Types of Signals

• Continuous-Time Signal
• Discrete-Time Signal
• Periodic Signal
• Orthogonal Signal
• Even and Odd Signal
• Energy Signal & Power Signal

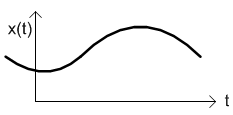
Continuous Time Signal

If the independent variable (t) is continuous, then the corresponding signal is continuous time signal.

 

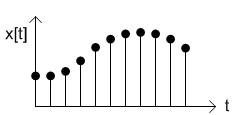
Discrete Time Signal

If the independent variable (t) takes on only discrete values, for example t = ±1, ±2, ±3, ...

 

Periodic Signal

If the transformed signal is same as x(t), then the signal is periodic.

where T is fundamental period (the smallest period) of signal x(t)

In discrete-time, the periodic signal is;

 

Orthogonal Signal

Each component signal has no relationship with others.
Orthogonal signal is denoted as φ(t).
 

Even and Odd Signal

One of characteristics of signal is symmetry that may be useful for signal analysis. Even signals are symmetric around vertical axis, and Odd signals are symmetric about origin.

Even Signal:
A signal is referred to as an even if it is identical to its time-reversed counterparts; x(t) = x(-t).

Odd Signal:
A signal is odd if x(t) = -x(-t).
An odd signal must be 0 at t=0, in other words, odd signal passes the origin.

Using the definition of even and odd signal, any signal may be decomposed into a sum of its even part, x_e(t), and its odd part, x_o(t), as follows:

It is an important fact because it is relative concept of Fourier series. In Fourier series, a periodic signal can be broken into a sum of sine and cosine signals. Notice that sine function is odd signal and cosine function is even signal.

Example

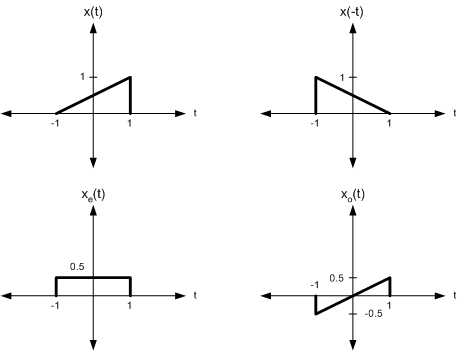
Energy Signal & Power Signal

In physics, energy is work and power is work per time;
Work = Force × Displacement
Power = Work / Time

For Kinetic energy is given by

In an electrical signal, the instantaneous power for the voltage across the resistance R and its energy are defined;

In signal processing, total energy of signal x(t) is defined as similar way;
(Notice that it is square of absolute value.)

where |x(t)| denotes the magnitude of x(t). It is necessary to get a scalar quantity for complex signal, because magnitude of complex number is defined as .

And, it is also squared because of common convention to use similar terminology for any signal (look at the definitions of kinetic and electrical signal energy). Therefore, the energy of a signal is defined as a sum of square of magnitude.

The average power of signal is defined by;

A signal can be categorized into energy signal or power signal: An energy signal has a finite energy, 0 < E < ∞. In other words, energy signals have values only in the limited time duration. For example, a signal having only one square pulse is energy signal. A signal that decays exponentially has finite energy, so, it is also an energy signal. The power of an energy signal is 0, because of dividing finite energy by infinite time (or length).

On the contrary, the power signal is not limited in time. It always exists from beginning to end and it never ends. For example, sine wave in infinite length is power signal. Since the energy of a power signal is infinite, it has no meaning to us. Thus, we use power (energy per given time) for power signal, because the power of power signal is finite, 0 < P < ∞.

Examples

1)
E = 1, and , ∴ Energy signal.

2)
E = ∞ , and , ∴ Power signal.