OpenGL Angles to Axes
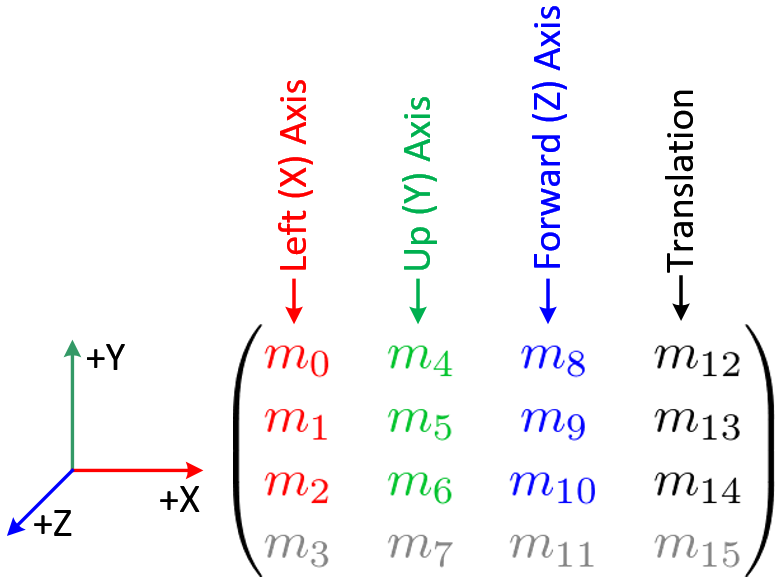
The rotation angles directly affect the first 3 columns of OpenGL GL_MODELVIEW matrix, precisely left, up and forward axis elements. For example, if a unit vector along X axis, (1, 0, 0) is multiplied by an arbitrary 3x3 rotation matrix, then the result of the vector after multiplication is (m0, m1, m2);
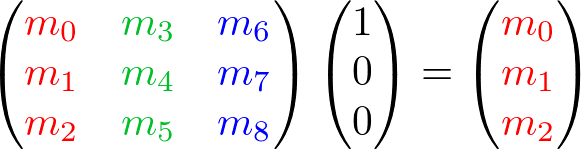
It means the first column (m0, m1, m2) of the rotation matrix represents the coordinates of the left axis after rotated. Similarly, the second column is the up axis and the third column is the forward axis.
This article describes how to contruct GL_MODELVIEW matrix with rotation angles.
Axis Rotations
First, we look at a rotation around each axis; +X, +Y and +Z. We project three axes onto a plane in 3 different ways, so the axis that we want to rotate is facing toward you. The positive rotation direction becomes counter clockwise (right hand rule).
Rotation about Left(X) Axis: Pitch
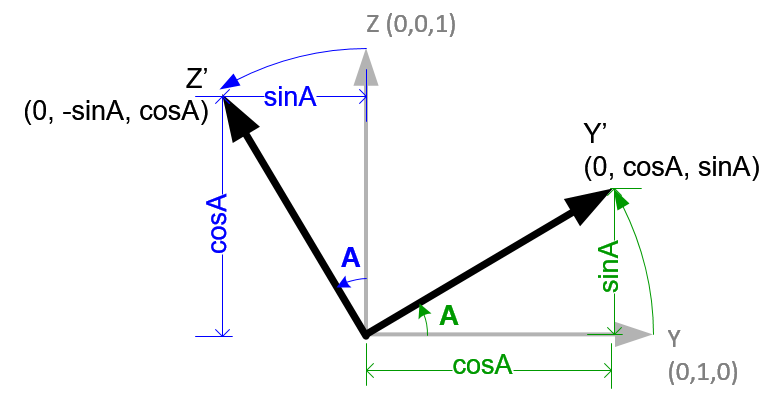
Initial value of up(Y) and forward(Z) axes are (0, 1, 0) and (0, 0, 1). If left(X) axis rotates A degree, then new up(Y') axis becomes (0, cosA, sinA) and forward(Z') becomes (0, -sinA, cosA). The new axes are inserted as column components of the 3x3 rotation matrix. Then, the rotation matrix becomes;
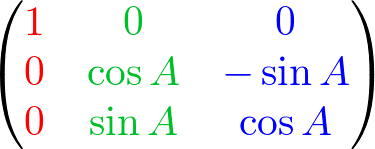
Rotation about Up(Y) Axis: Yaw, Heading
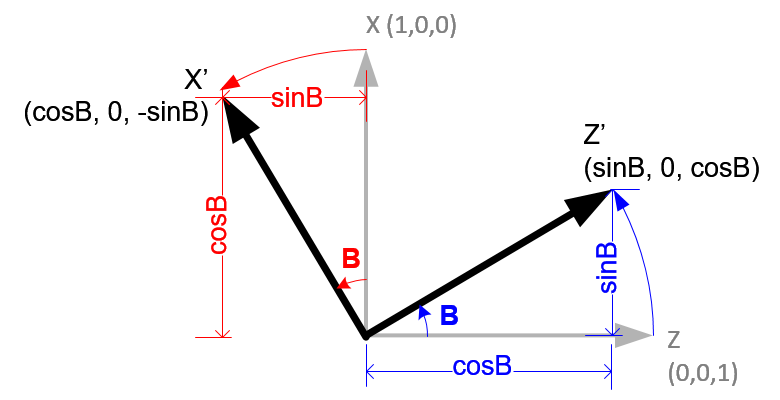
Now, we rotate around up vector, which is facing toward you, with B angle . Left(X) axis is transformed from (1, 0, 0) to X' (cosB, 0, -sinB). And forward(Z) axis is from (0, 0, 1) to Z' (sinB, 0, cosB).
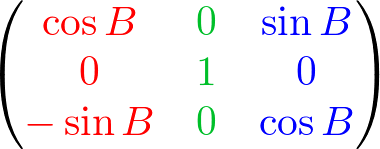
Rotation about Forward(Z) Axis: Roll
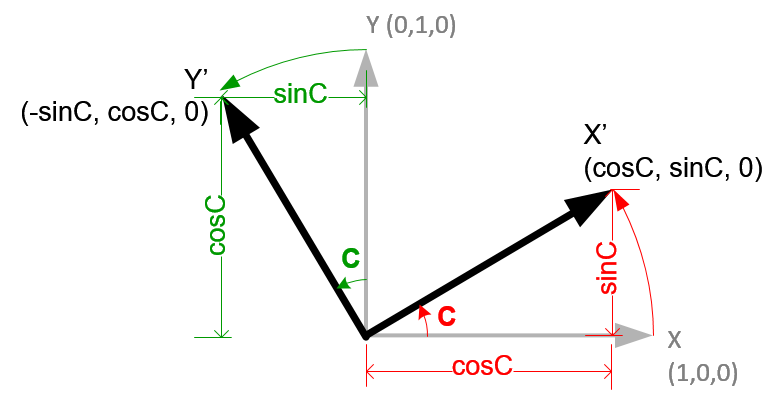
If we rotate forward(Z) axis with angle C degree, the original left(X) (1, 0, 0) axis becomes X' (cosC, sinC, 0), and up(Y) (0, 1, 0) axis becomes Y' (-sinC, cosC, 0).
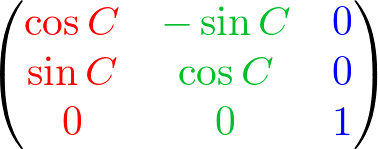
Angles To Axes
We can combine these separate axis rotations into one matrix by multiplying the above 3 matrices together. Note that multiplication of matrices is not commutative, so a different order of matrix multiplication results in a different outcome. There are 6 different combinations are possible; RxRyRz, RxRzRy, RyRxRz, RyRzRx, RzRxRy and RzRyRx.
The left column of the combined rotation matrix is the left axis after rotated, the middle column is the up axis, and the right column is the forward axis.
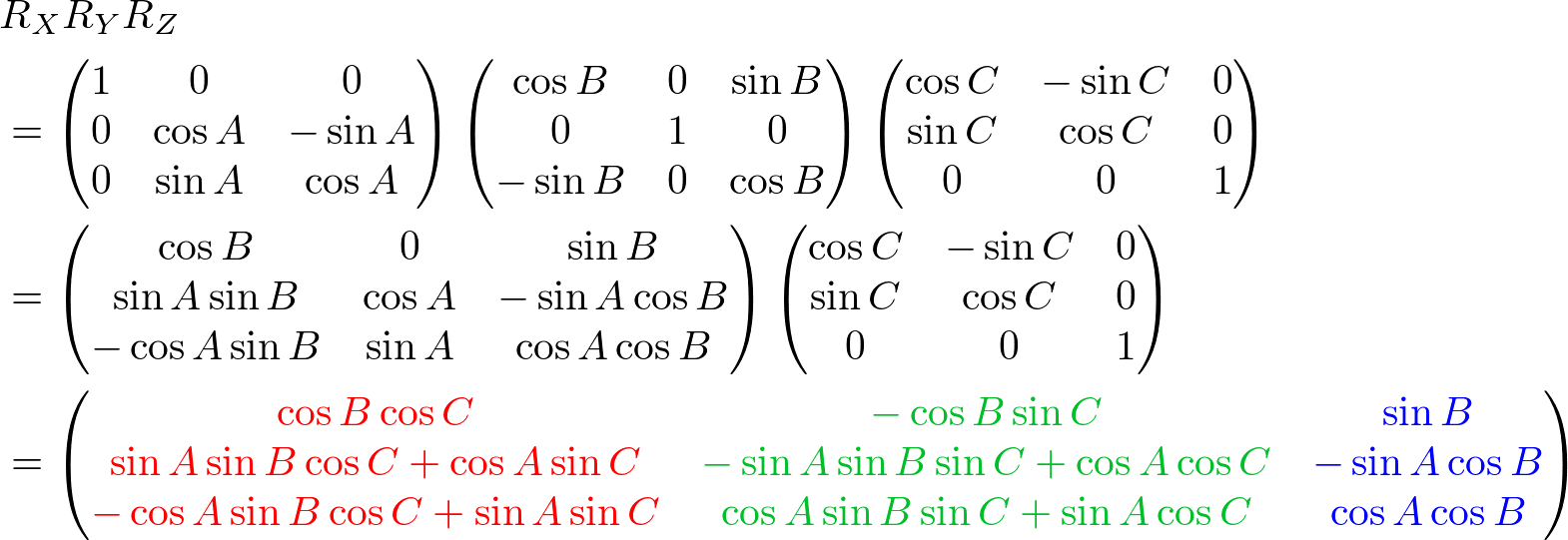
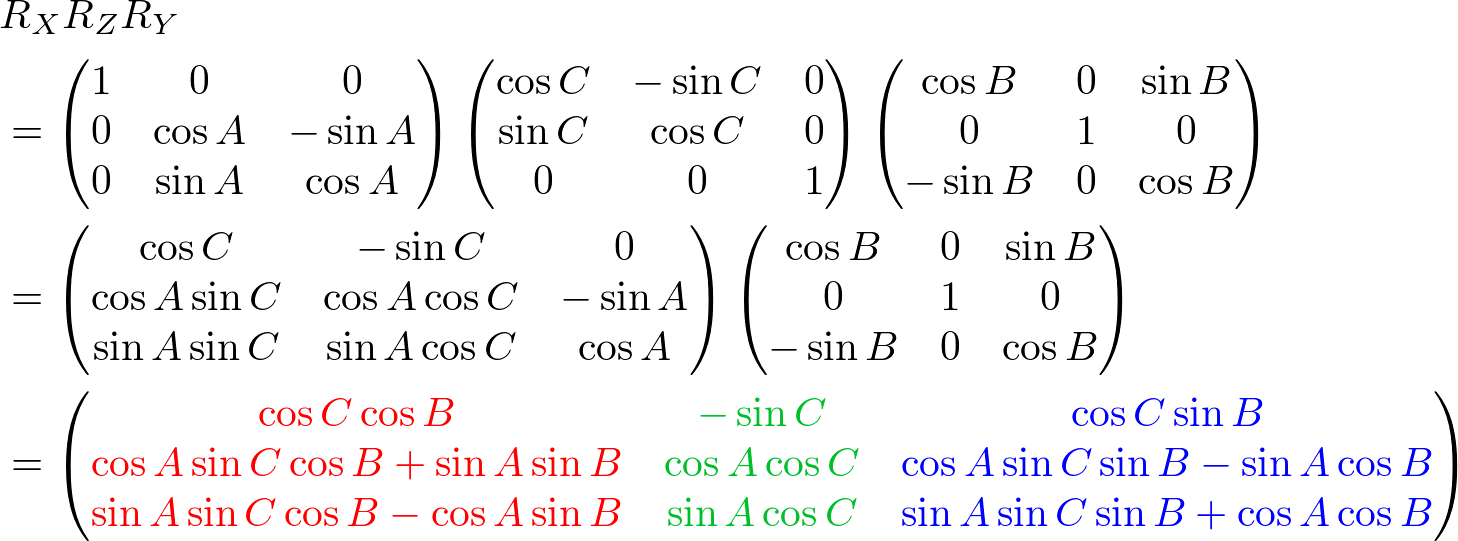
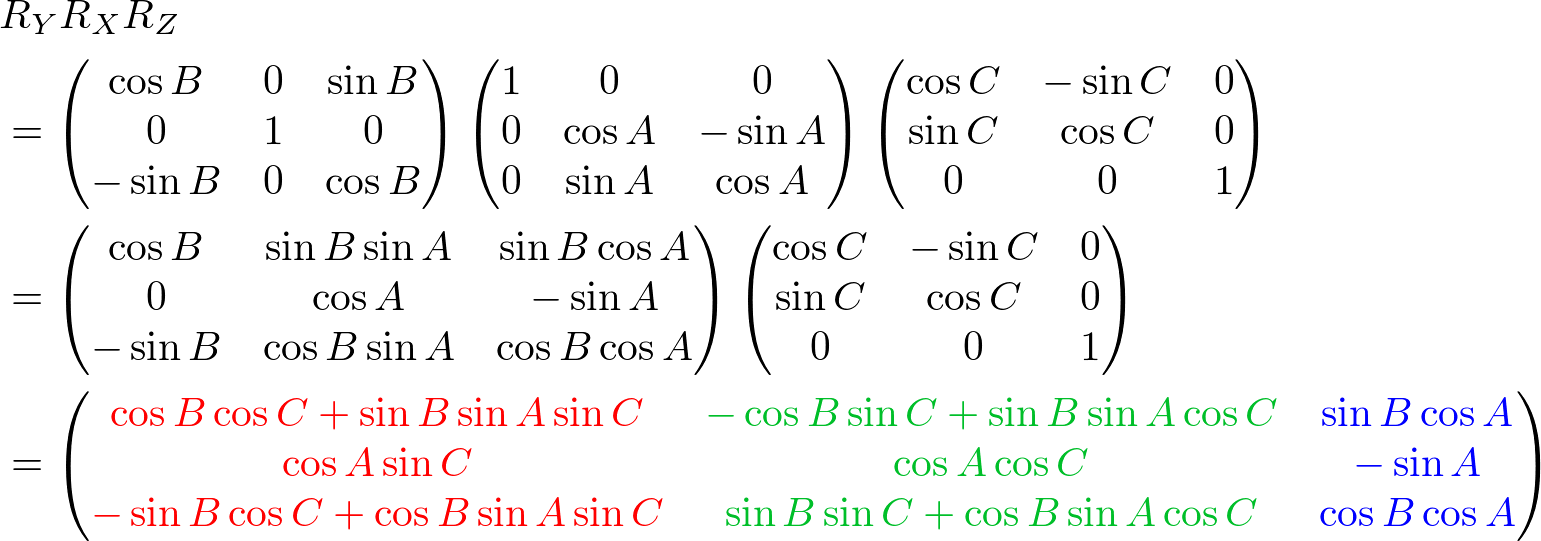
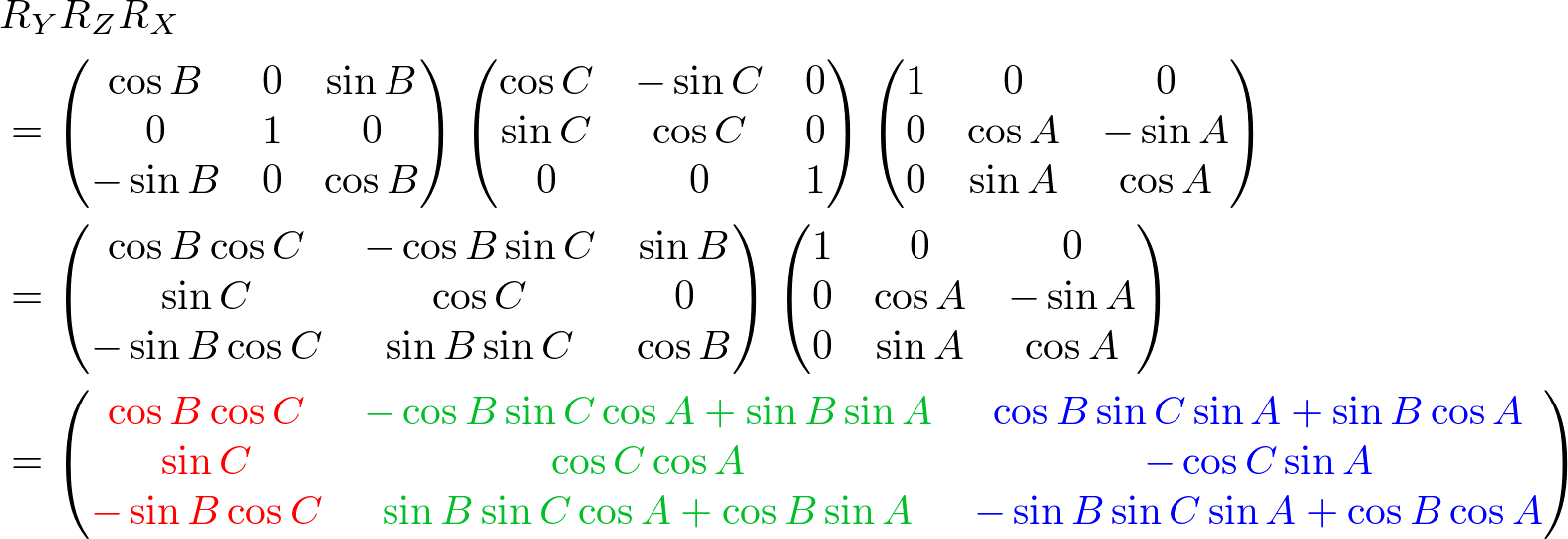
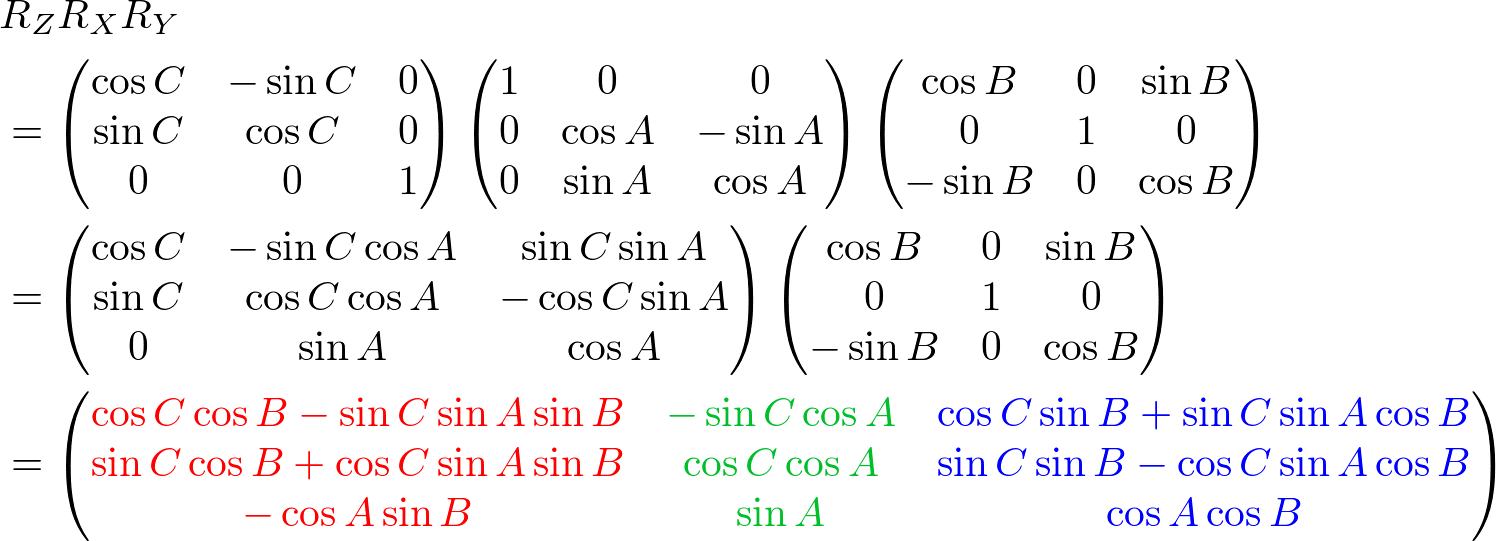
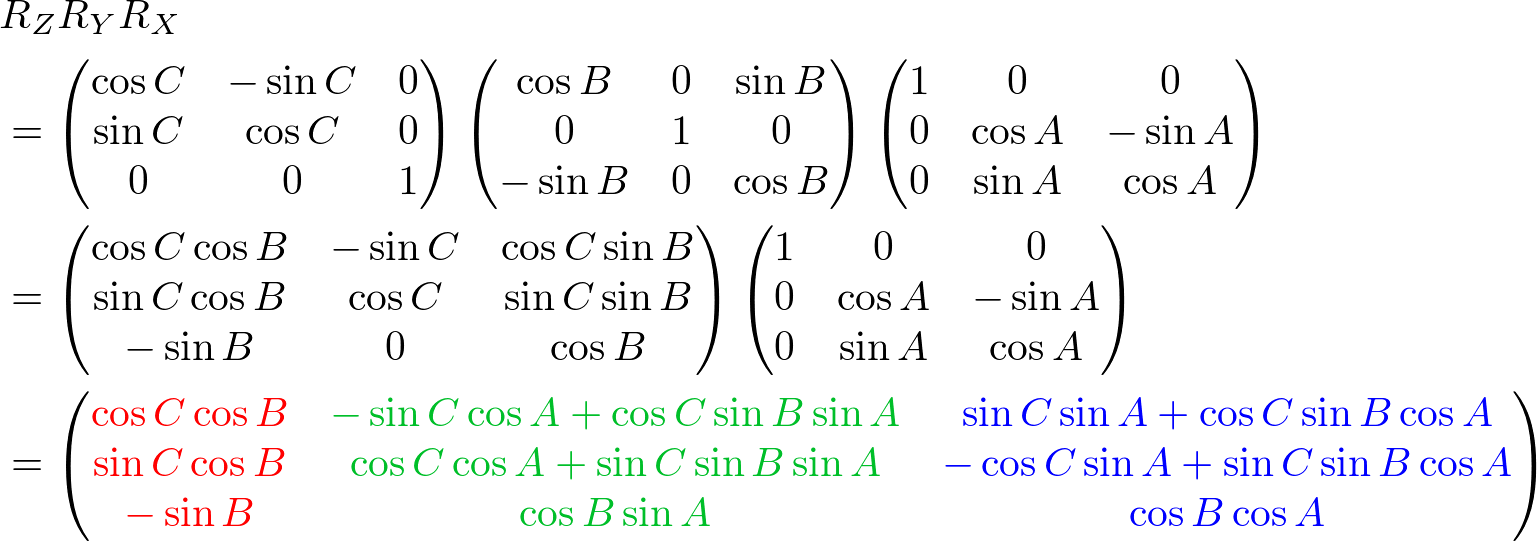
Here is a C++ example code for RxRyRz combination. It performs 3 rotations in order of Rz (roll), Ry (yaw) then Rx (pitch). The results of left, up and forward axis can be used to construct GL_MODELVIEW matrix.
// minimal implimentation of Vector3 struct
struct Vector3
{
float x;
float y;
float z;
Vector3() : x(0), y(0), z(0) {}; // initialze when created
};
///////////////////////////////////////////////////////////////////////////////
// convert Euler angles(x,y,z) to axes(left, up, forward)
// Each column of the rotation matrix represents left, up and forward axis.
// The order of rotation is Roll->Yaw->Pitch (Rx*Ry*Rz)
// Rx: rotation about X-axis, pitch
// Ry: rotation about Y-axis, yaw(heading)
// Rz: rotation about Z-axis, roll
// Rx Ry Rz
// |1 0 0| | Cy 0 Sy| |Cz -Sz 0| | CyCz -CySz Sy |
// |0 Cx -Sx|*| 0 1 0|*|Sz Cz 0| = | SxSyCz+CxSz -SxSySz+CxCz -SxCy|
// |0 Sx Cx| |-Sy 0 Cy| | 0 0 1| |-CxSyCz+SxSz CxSySz+SxCz CxCy|
///////////////////////////////////////////////////////////////////////////////
void anglesToAxes(const Vector3 angles, Vector3& left, Vector3& up, Vector3& forward)
{
const float DEG2RAD = acos(-1) / 180.0f; // PI/180
float sx, sy, sz, cx, cy, cz, theta;
// rotation angle about X-axis (pitch)
theta = angles.x * DEG2RAD;
sx = sin(theta);
cx = cos(theta);
// rotation angle about Y-axis (yaw)
theta = angles.y * DEG2RAD;
sy = sin(theta);
cy = cos(theta);
// rotation angle about Z-axis (roll)
theta = angles.z * DEG2RAD;
sz = sin(theta);
cz = cos(theta);
// determine left axis
left.x = cy*cz;
left.y = sx*sy*cz + cx*sz;
left.z = -cx*sy*cz + sx*sz;
// determine up axis
up.x = -cy*sz;
up.y = -sx*sy*sz + cx*cz;
up.z = cx*sy*sz + sx*cz;
// determine forward axis
forward.x = sy;
forward.y = -sx*cy;
forward.z = cx*cy;
}