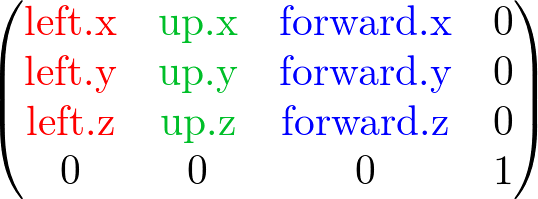OpenGL Lookat to Axes

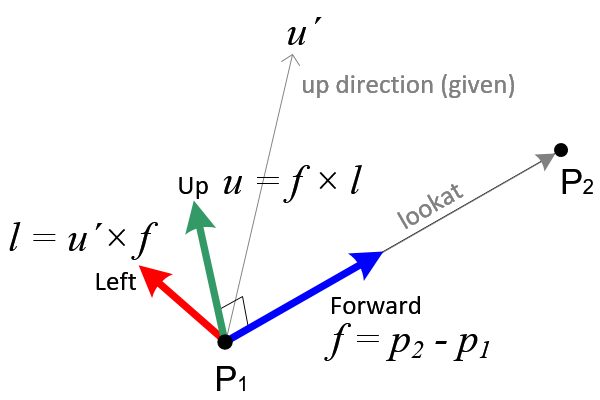
The rotation matrix can be constructed by a lookat vector with 2 or 3 points in 3D space. If an object at P₁ is facing to P₂, then the lookat vector is P₂ - P₁.

First, Forward axis vector is simply calculated by normalizing the lookat vector.

Second, left axis vector is computed by a cross product of a specified up direction vector and forward axis. This up direction vector is given to determine the roll angle of the object. And, it is not necessary perpendicular to the forward axis. If we don't consider roll rotation of the object, then we can use (0, 1, 0) instead. It means the object is always stood straight up.

The actual up axis vector, which is orthogonal to both forward and left axis, is computed by another cross product of forward and left. Both left and up axis should be normalized after cross product in order to have a unit length.

Here is a C++ example to calculate left, up and forward axis from a lookat vector. The first code block is a minimal implementation of Vector3 struct variable. The second code block is to compute 3 axes from 2 points (position and target vectors), and the last code block is to compute 3 axes from 3 points (position, target and up direction vectors).

// minimal implementation of Vector3 struct
struct Vector3
{
    float x;
    float y;
    float z;

    Vector3() : x(0), y(0), z(0) {};              // constructors
    Vector3(float x, float y, float z) : x(x), y(y), z(z) {};

    // functions
    Vector3& normalize();                         //
    Vector3  operator-(const Vector3& rhs) const; // subtract rhs
    Vector3  operator*(const Vector3& rhs) const; // cross product
    Vector3& operator*=(const float scale);       // scale and update itself
};

Vector3& Vector3::normalize() {
    float invLength = 1 / sqrtf(x*x + y*y + z*z);
    x *= invLength;
    y *= invLength;
    z *= invLength;
    return *this;
}

Vector3 Vector3::operator-(const Vector3& rhs) const {
    return Vector3(x-rhs.x, y-rhs.y, z-rhs.z);
}

Vector3 Vector3::operator*(const Vector3& rhs) const {
    return Vector3(y*rhs.z - z*rhs.y, z*rhs.x - x*rhs.z, x*rhs.y - y*rhs.x);
}

Vector3& Vector3::operator*=(const float a) {
    x *= a; y *= a; z *= a;
    return *this;
}

///////////////////////////////////////////////////////////////////////////////
// compute transform axis from object position and target point
///////////////////////////////////////////////////////////////////////////////
void lookAtToAxes(const Vector3& position, const Vector3& target,
                  Vector3& left, Vector3& up, Vector3& forward)
{
    // compute the forward vector
    forward = target - position;
    forward.normalize();

    // compute temporal up vector based on the forward vector
    // watch out when look up/down at 90 degree
    // for example, forward vector is on the Y axis
    if(fabs(forward.x) < EPSILON && fabs(forward.z) < EPSILON)
    {
        // forward vector is pointing +Y axis
        if(forward.y > 0)
            up = Vector3(0, 0, -1);
        // forward vector is pointing -Y axis
        else
            up = Vector3(0, 0, 1);
    }
    // in general, up vector is straight up
    else
    {
        up = Vector3(0, 1, 0);
    }

    // compute the left vector
    left = up * forward;  // cross product
    left.normalize();

    // re-calculate the orthonormal up vector
    up = forward * left;  // cross product
    up.normalize();
}

///////////////////////////////////////////////////////////////////////////////
// compute transform axis from object position, target and up direction
///////////////////////////////////////////////////////////////////////////////
void lookAtToAxes(const Vector3& pos, const Vector3& target, const Vector3& upDir,
                  Vector3& left, Vector3& up, Vector3& forward)
{
    // compute the forward vector
    forward = target - pos;
    forward.normalize();

    // compute the left vector
    left = upDir * forward;  // cross product
    left.normalize();

    // compute the orthonormal up vector
    up = forward * left;  // cross product
    up.normalize();
}

←Back