OpenGL Matrix Class (C++)

Related Topics: OpenGL Transform, OpenGL Projection Matrix, Quaternion To Rotation Matrix, Rotation About Axis
Download: matrix.zip, matrix_rowmajor.zip

Overview

OpenGL fixed pipeline provides 4 different types of matrices (GL_MODELVIEW, GL_PROJECTION, GL_TEXTURE and GL_COLOR) and transformation routines for these matrices; glLoadIdentity(), glTranslatef(), glRotatef(), glScalef(), glMultMatrixf(), glFrustum() and glOrtho().

These built-in matrices and routines are useful to develop simple OpenGL applications and to understand the matrix transformation. But once your application is getting complicated, it is better to manage your own matrix implementations by yourself for all movable objects. Furthermore, you cannot use these built-in matrix functions anymore in OpenGL programmable pipeline (GLSL) such as OpenGL v3.0+, OpenGL ES v2.0+ and WebGL v1.0+. You must have your own marix implementations then pass the matrix data to OpenGL shaders.

This article provides a stand-alone, general purpose 4x4 matrix class, Matrix4 written in C++, and describes how to integrate this matrix class to the OpenGL applications. This matrix class is only dependent on its sister classes; Vector3 and Vector4 defined Vectors.h. These vector classes are also included in matrix.zip.

Matrix4 Creation & Initialization

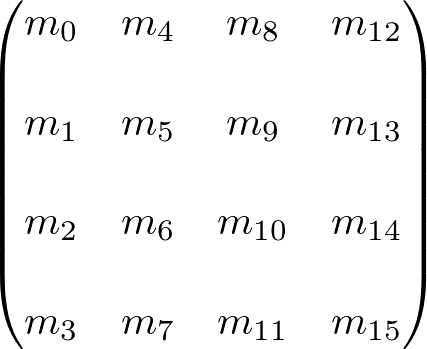
Column-major order 4x4 Matrix
Matrix4 uses column-major

Matrix4 class contains an array of float data type to store 16 elements of 4x4 square matrix, and has 3 constructors to instantiate a Matrix4 class object.

Matrix4 class uses the column-major order notation same as OpenGL uses. (Array elements are filled in the first column first and move on the second column.) Note that row-major and column-major order are just different ways to store multi-dimensional arrays into a linear (one-dimensional) memory space, and the results of matrix arithmetic and operations are no difference.

With default constructor (with no argument), Matrix4 object is created as an identity matrix. Other 2 constructors take either 16 arguments or an array of 16 elements. You may also use the copy constructor and assignment operator (=) to initialize a Matrix4 object.

By the way, the copy constructor and assignment operator will be automatically generated by C++ compiler for you.

Here are example codes to construct Matrix4 objects in various ways. First, include Matrices.h in your code before using Matrix4 class. 


#include "Matrices.h"   // for Matrix2, Matrix3, Matrix4
...

// create an identity matrix with default ctor
Matrix4 m1;

// create a matrix with 16 elements
Matrix4 m2(1, 1, 1, 1,   // 1st column
           1, 1, 1, 1,   // 2nd column
           1, 1, 1, 1,   // 3rd column
           1, 1, 1, 1);  // 4th column

// create a matrix with an array
float a[16] = {2,2,2,2, 2,2,2,2, 2,2,2,2, 2,2,2,2};
Matrix4 m3(a);

// create a matrix with copy ctor
Matrix4 m4(m3);          // m3 and m4 have same elements now
Matrix4 m5 = m3;         // m3 and m5 have same elements now
...

Matrix4 Accessors (Setters/Getters)

Setters

Matrix4 class provides set() method to set all 16 elements. 


Matrix4 m1;

// set matrix with 16 float elements (column-major order)
m1.set(1,1,1,1, 1,1,1,1, 1,1,1,1, 1,1,1,1);

// set matrix with an array
float a1[] = {2,2,2,2, 2,2,2,2, 2,2,2,2, 2,2,2,2};
m1.set(a1);

You can also set the column or row elements at once with setRow() or setColumn(). The first param of setRow() and setColumn() is the zero-based index (0, 1, 2, or 3) value. The second param is the pointer to the array containing 4 elements. 


Matrix4 m2;
float a2[4] = {2,2,2,2};

// set a row with the row index and array
m2.setRow(0, a2);      // 1st row

// set a column with the column index and array
m2.setColumn(2, a2);   // 3rd column

You can also set an individual matrix element using [ ] operator. Please see Access Individual Element section. 


// set each element of matrix
Matrix4 m3;
m3[0] = 1.0f;          // set 1st element
m3[1] = 1.0f;          // set 2nd element
m3[2] = 1.0f;          // set 3rd element
...

Identity Matrix

Matrix4 class has a special setter, identity() to make an identity matrix. 


// set identity matrix
Matrix4 m3;
m3.identity();

Getters

Matrix4::get() method returns the pointer to the array of 16 elements. And, getTranspose() returns the transposed matrix elements. Or, use transpose() if you want to convert the current matrix to be transposed. The transpose matrix is typically used to find the inverse matrix of an Euclidean transform matrix. More details are in the example. 


// get matrix elements as an array ptr
Matrix4 m4;
const float* a = m4.get();
const float* b = m4.getTranspose();   // returns transposed matrix elements

// pass matrix to OpenGL
glLoadMatrixf(m4.get());

// pass matrix to GLSL
glUniformMatrix4fv(location, 1, false, m4.get());

You can also get the column or row elements as Vector4 with getRow() or getColumn(). The parameter of getRow() and getColumn() is the zero-based index (0, 1, 2, or 3) value of the selected row or column.

There are also getLeftAxis(), getUpAxis() and getForwardAxis() functions to get left/up/forward vectors as Vector3. 


Matrix4 m4;

// get a row with the row index
Vector4 v1 = m4.getRow(0);             // 1st row

// get a column with the column index
Vector4 v2 = m4.getColumn(2);          // 3rd column

// get left/up/forward vectors
Vector3 left    = m4.getLeftAxis();    // left vector
Vector3 up      = m4.getUpAxis();      // up vector
Vector3 forward = m4.getForwardAxis(); // forward vector

Access Individual Element

An individual element of a matrix can be also accessible by the subscript operator, [ ]. 


Matrix4 m5;
float f = m5[0];    // get 1st element

m5[1] = 2.0f;       // set 2nd element

Get Rotation Angle

getAngle() returns 3 Euclidean angles; pitch, yaw and roll in degree, range between -180 ~ +180 from the current matrix.

  • Pitch: Rotation about X-axis
  • Yaw: Rotation about Y-axis
  • Roll: Rotation about Z-axis

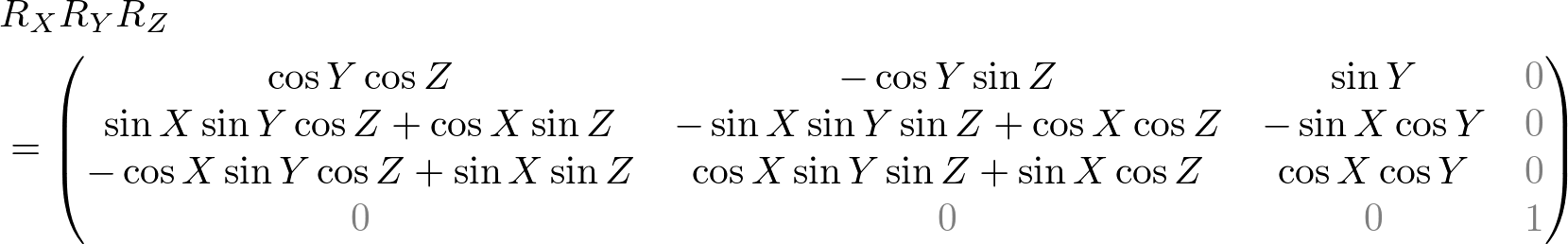
getAngle() function assumes the order of rotations is Roll ➔ Yaw ➔ Pitch. If roll is Z, yaw is Y and pitch is X angle, then the combined rotation matrix for this order would be; rotation matrix by RxRyRz
From 9th element of matrix, m[8]=sinY, you can find the yaw angle first by using inverse sine. Then, the roll angle can be found by inverting tangent of m[0] and m[4] elements, atan(-m[4]/m[0]). Finally, the pitch angle can be computed by inverting tangent of m[9] and m[10], atan(-m[9]/m[10]). Please look at the detail algorithm to find all 3 angles in Matrix.cpp. 


Matrix4 m6(...);                        // set any rotation
Vector3 angle = m6.getAngle();          // get angle(rx, ry, rz) in degree

std::cout << angle.x << std::endl;      // pitch
std::cout << angle.y << std::endl;      // yaw
std::cout << angle.z << std::endl;      // roll

Print Matrix4

Matrix4 also provides a handy print function with std::ostream operator <<, for debugging purpose. 


// print matrix
Matrix4 m7;
std::cout << m7 << std::endl;

// output should look like
[   1.00000    0.00000    0.00000    0.00000]
[   0.00000    1.00000    0.00000    0.00000]
[   0.00000    0.00000    1.00000    0.00000]
[   0.00000    0.00000    0.00000    1.00000]

Matrix4 Arithmetic

Matrix4 class provides basic arithmetic (+, -, *) between 2 matrices.

Addition & Subtraction

You can add or subtract 2 matrices. 


Matrix4 m1, m2, m3;

// addition
m3 = m1 + m2;
m3 += m1;       // short-hand op: m3 = m3 + m1

// subtract
m3 = m1 - m2;
m3 -= m1;       // short-hand op: m3 = m3 - m1

Multiplication

You can multiply 2 matrices together, and there are multiplications with scalar or 3D/4D vector as well, to transform the vector with the matrix. Note that matrix multiplication is not commutative. 


Matrix4 m1, m2, m3;

// matrix multiplication
m3 = m1 * m2;
m3 *= m1;       // short-hand op: m3 = m3 * m1

// scalar product
m3 = 2 * m1;    // scale all elements by 2

// vector multiplication
Vector3 v1, v2;
v2 = m1 * v1;   // post-multiplication
v2 = v1 * m1;   // pre-multiplication

Comparison

Matrix4 class provides comparison operators to compare all elements of 2 matrices. 


Matrix4 m1, m2;

// exact comparison with no epsilon
if(m1 == m2)
    std::cout << "equal" << std::endl;
if(m1 != m2)
    std::cout << "not equal" << std::endl;

Matrix4 Transform Functions

OpenGL has several fuctions for matrix transformations; glTranslatef(), glRotatef() and glScalef(). Matrix4 class provides the equivalent functions to transform matrix; translate(), rotate() and scale() respectively. In addition, Matrix4 provides invert() to compute a inverse matrix.

Matrix4::translate(x, y, z)

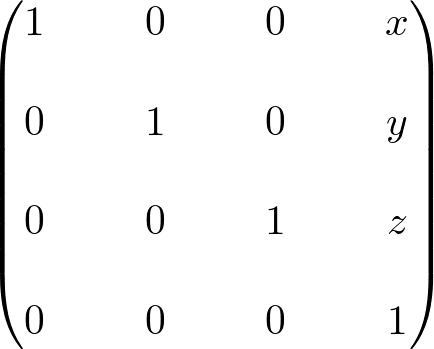
translation matrix
Translation Matrix, MT

translate() produces the current matrix translated by (x, y, z). First, it creates a translation matrix, MT, then multiplies it with the current matrix object to produce the final transform matrix:

Note that this function is equivalent to OpenGL's glTranslatef(), but OpenGL uses post-multiplication instead of pre-multiplication (The translation matrix is multiplied back of the current matrix.) . If you apply multiple transforms, then the result is significantly different because matrix multiplication is not commutative.

Please see more examples of ModelView Matrix for applying sequential transforms. 


// M1 = Mt * M1
Matrix4 m1;
m1.translate(1, 2, 3);   // move to (x, y, z)

Matrix4::rotate(angle, x, y, z)

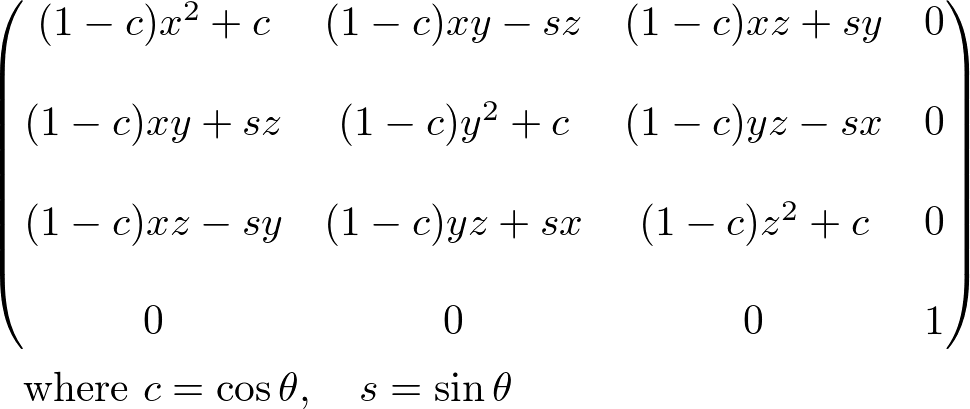
rotation matrix
Rotation Matrix, MR

rotate() can be used to rotate 3D models by an angle (degree) about a rotation axis (x, y, z). This function generates a rotation matrix MR, then multiplies it with the current matrix object to produce the final rotation transform matrix:

The derivation of this rotation matrix is described here.
Rotation About Arbitrary Axis

It is equivalent to glRotatef(), but OpenGL uses post-multiplication to produce the final transform matrix:

rotate() is for rotation on an arbitary axis. Matrix4 class provides additional 3 functions for basis axis rotation; rotateX(), rotateY(), and rotateZ(). 


// M1 = Mr * M1
Matrix4 m1;
m1.rotate(45, 1,0,0);   // rotate 45 degree about x-axis
m1.rotateX(45);         // same as rotate(45, 1,0,0)

It is possible to get the equivalent rotation matrix using Quaternion. See the detail in Quaternion to Rotation Matrix page.

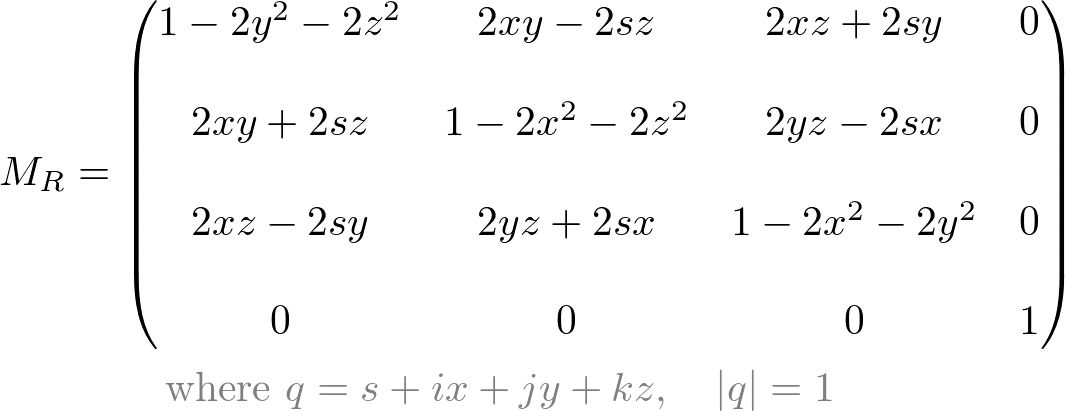
4x4 rotation matrix
Rotation Matrix from Quaternion Multiplication, qpq*

Matrix4::lookAt()

lookAt() function rotates the current matrix to look at the given target point. This function can be used to rotate an object always facing to the camera (or view), such as billboard or sprite. Note that this function clears the previous 3x3 rotation component of the matrix, and re-computes it with target point. But, the translation component (4th column of the matrix) remains unchanged. 


Vector3 target(1, 2, 3); // target point
Matrix4 m1;
m1.lookAt(target);       // rotate it to the target

Note that it is for rotating an object, but not for camera. To implement camera's lookAt function, see camera's lookAt()

Matrix4::scale(x, y, z)

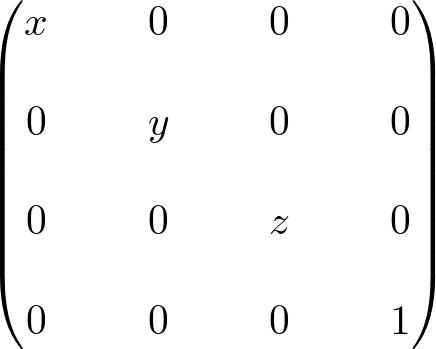
scale matrix
Scaling Matrix, MS

scale() produces a non-uniform scaling transform matrix on each axis (x, y, z) by multiplying the current matrix object and scaling matrix: .

Note again, OpenGL's glScalef() performs post-multiplication: .

Matrix4 class also provides uniform scaling function as well. 


// M1 = Ms * M1
Matrix4 m1;
m1.scale(1,2,3);    // non-uniform scale
m1.scale(4);        // uniform scale (same on all axis)

Matrix4::invert()

invert() function computes the inverse of the current matrix. This inverse matrix is typically used to transform the normal vectors from object space to eye space. Normals are transformed differently as vertices do. Normals are multiplied by the inverse of GL_MODELVIEW matrix to transform to eye space, . The detail is explained here.

If the matrix is only Euclidean transform (rotation and translation), or Affine transform (in addition, scaling and shearing), then the computation of inverse matrix is much simpler. Matrix4::invert() will determine the appropriate inverse method for you, but you can explicitly call a specific inverse function; invertEuclidean(), invertAffine(), invertProjective() or invertGeneral(). Please look at the detail descriptions in Matrices.cpp file. 


Matrix4 m1;
m1.invert();    // inverse matrix

Example: ModelView Matrix

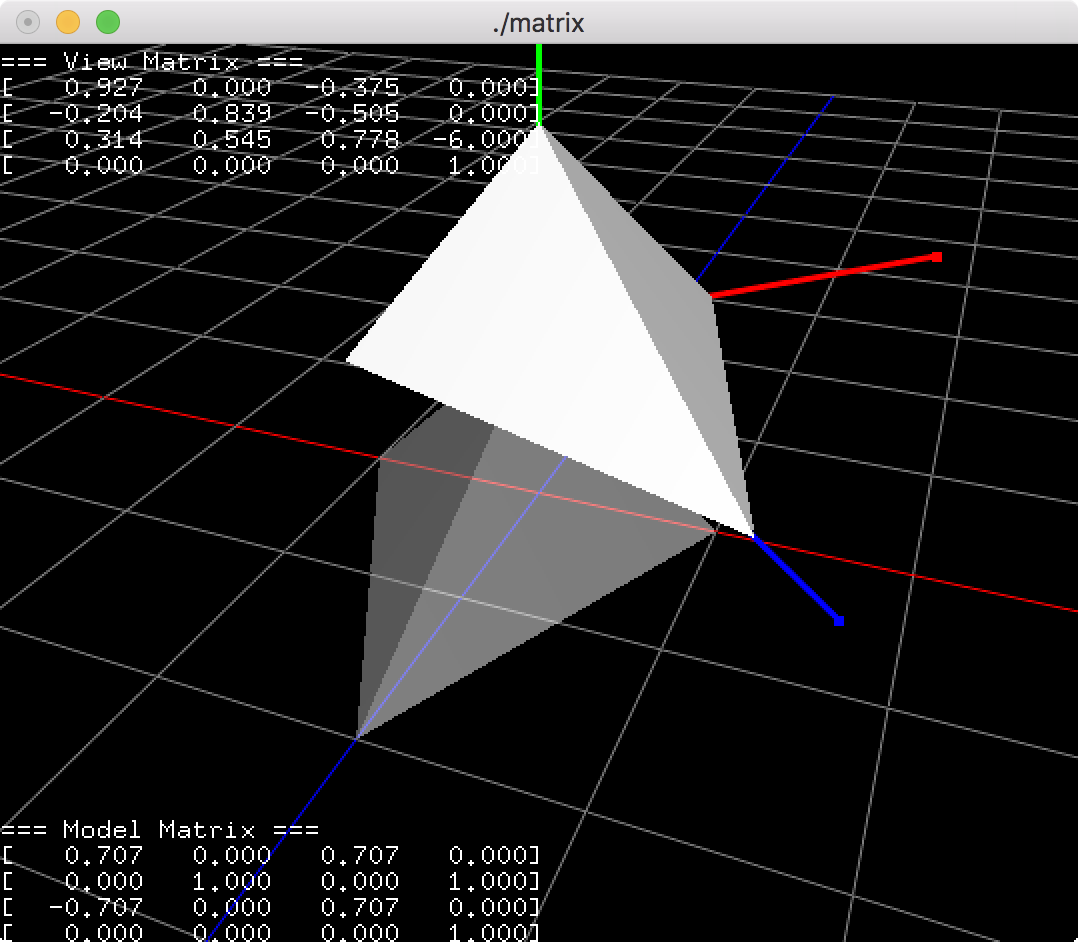
Download the source and binary: matrix.zip (Updated: 2020-03-26)

This example shows how to integrate Matrix4 class with OpenGL. GL_MODELVIEW matrix combines the view matrix and model matrix, but we keep them separately and pass the product of these 2 matrices to OpenGL's GL_MODELVIEW when it is required. 


Matrix4 matModel, matView, matModelView;
glMatrixMode(GL_MODELVIEW);
...

// orbital camera (view)
matView.identity();                 // transform orders:
matView.rotate(-camAngleY, 0,1,0);  // 1st: rotate on y-axis
matView.rotate(-camAngleX, 1,0,0);  // 2nd: rotate on x-axis
matView.translate(0, 0, -camDist);  // 3rd: translate along z

// model transform:
// rotate 45 on Y-axis then move 2 unit up
matModel.identity();
matModel.rotate(45, 0,1,0);         // 1st transform
matModel.translate(0, 2, 0);        // 2nd transform

// build modelview matrix: Mmv = Mv * Mm
matModelView = matView * matModel;

// pass it to opengl before draw
glLoadMatrixf(matModelView.get());

// draw
...

The equivalent OpenGL implementatations are following. The transform result is same as above. 


// set the current matrix to GL_MODELVIEW
// any subsequent transforms will be directly applied to GL_MODELVIEW
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();

// orbital camera (view)
// NOTE: the order of transforms are reversed
//       because OpenGL uses post-multiplication
glTranslatef(0, 0, -camDist);       // 3rd: translate along z
glRotatef(-camAngleX, 1,0,0);       // 2nd: rotate on x-axis
glRotatef(-camAngleY, 0,1,0);       // 1st: rotate on y-axis

// model transform:
// rotate 45 on Y-axis then move 2 unit up
glTranslatef(0, 2, 0);              // 2nd transform
glRotatef(45, 0,1,0);               // 1st transform

// draw
...

The inverse of the modelview matrix is used for transforming the normals from object space to eye space. In programmable rendering pipeline, you may need to pass it to GLSL shader. 


// build transform matrix for normals: (M^-1)^T
Matrix4 matNormal = matModelView;   // copy from modelview matrix
matNormal.invert();                 // get inverse for normal transform
matNormal.transpose();              // transpose matrix

Example: Projection Matrix

This example shows how to build the projection matrix, equivalent to glFrustum() and glOrtho(). Please see the source codes for more details.

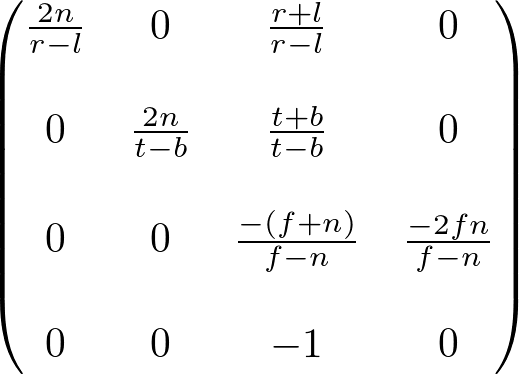
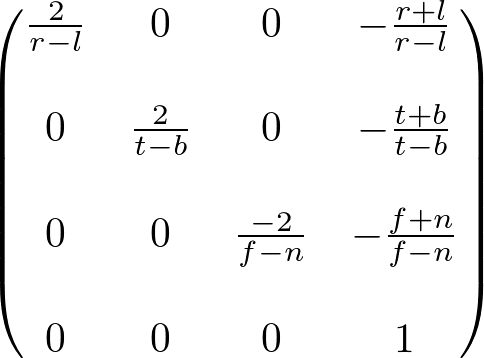
Perspective Projetion Matrix
Perspective Projection Matrix
Perspective Projetion Matrix
Orthographic Projection Matrix

If you want to know how the perspective and orthographic projection matrix is constructed in OpenGL, please read OpenGL Projection Matrix page. 


// set projection matrix and pass to opengl
// PARAMS: left, right, bottom, top, near, far
Matrix4 matProject = setFrustum(-1, 1, -1, 1, 1, 100);

glMatrixMode(GL_PROJECTION);
glLoadMatrixf(matProject.get());
...

///////////////////////////////////////////////////////////////////////////////
// equivalent to glFrustum()
// PARAMS: (left, right, bottom, top, near, far)
///////////////////////////////////////////////////////////////////////////////
Matrix4 setFrustum(float l, float r, float b, float t, float n, float f)
{
    Matrix4 mat;
    mat[0]  = 2 * n / (r - l);
    mat[5]  = 2 * n / (t - b);
    mat[8]  = (r + l) / (r - l);
    mat[9]  = (t + b) / (t - b);
    mat[10] = -(f + n) / (f - n);
    mat[11] = -1;
    mat[14] = -(2 * f * n) / (f - n);
    mat[15] = 0;
    return mat;
}

///////////////////////////////////////////////////////////////////////////////
// equivalent to gluPerspective()
// PARAMS: (vertical FOV, aspect ratio = width/height, near, far)
///////////////////////////////////////////////////////////////////////////////
Matrix4 setFrustum(float fovY, float aspect, float front, float back)
{
    float tangent = tanf(fovY/2 * DEG2RAD); // tangent of half fovY
    float height = front * tangent;         // half height of near plane
    float width = height * aspect;          // half width of near plane

    // params: left, right, bottom, top, near, far
    return setFrustum(-width, width, -height, height, front, back);
}

///////////////////////////////////////////////////////////////////////////////
// equivalent to glOrtho()
// PARAMS: (left, right, bottom, top, near, far)
///////////////////////////////////////////////////////////////////////////////
Matrix4 setOrthoFrustum(float l, float r, float b, float t, float n, float f)
{
    Matrix4 mat;
    mat[0]  = 2 / (r - l);
    mat[5]  = 2 / (t - b);
    mat[10] = -2 / (f - n);
    mat[12] = -(r + l) / (r - l);
    mat[13] = -(t + b) / (t - b);
    mat[14] = -(f + n) / (f - n);
    return mat;
}
...
←Back
 
Hide Comments
comments powered by Disqus