OpenGL Rotation About Arbitrary Axis

Related Topics: OpenGL Matrix, Quaternion to Matrix, Angles To Axes, Lookat To Axes
Download: rotate.zip

Derive Rodrigues' Formula

The 4x4 transformation matrix for rotating about an arbitrary axis in OpenGL is defined as;
4x4 matrix for rotating about arbitrary axis

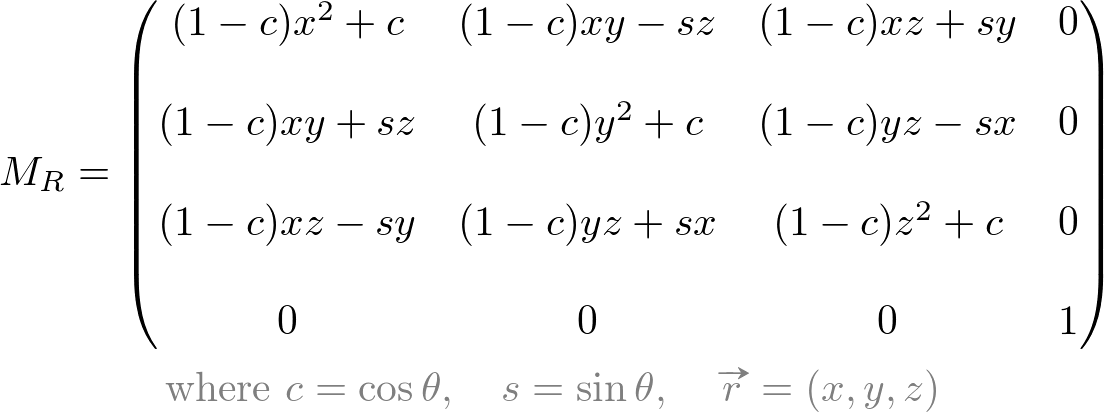
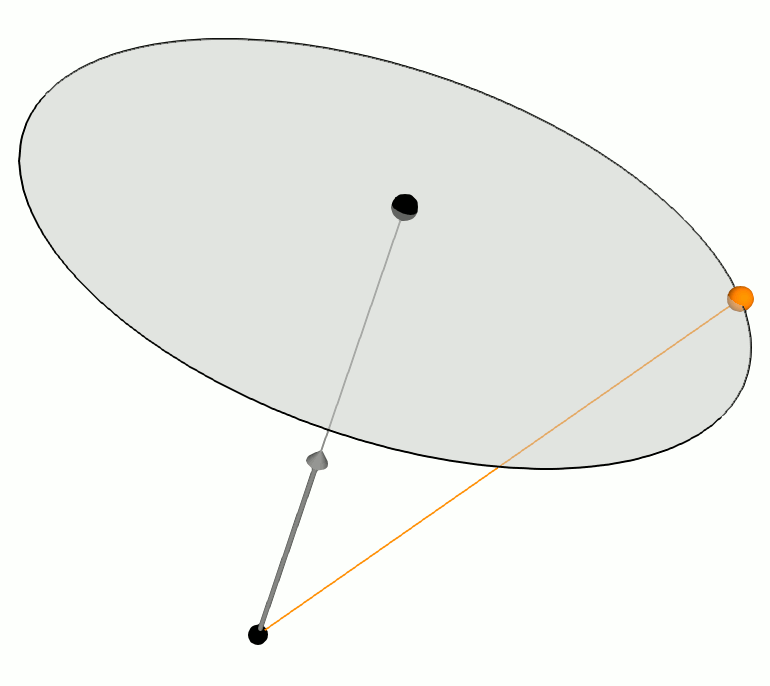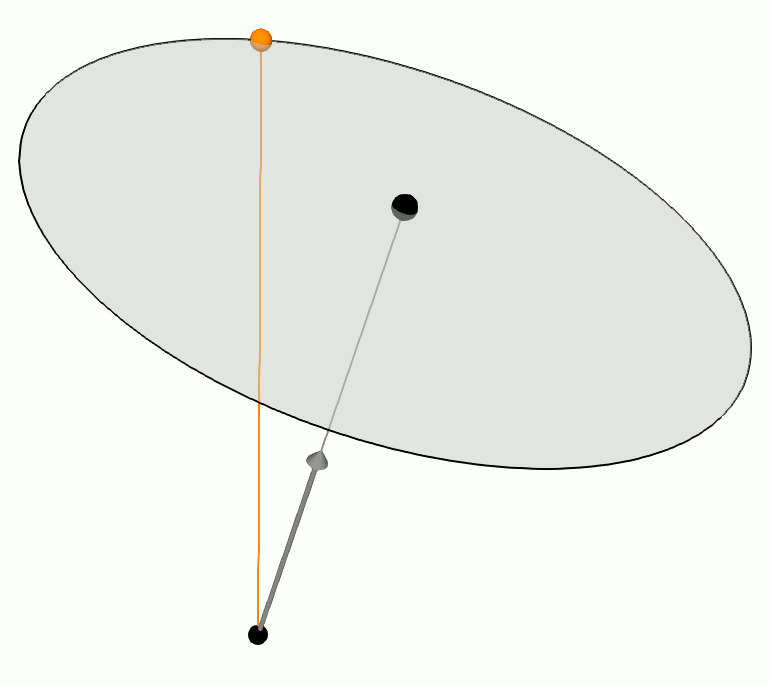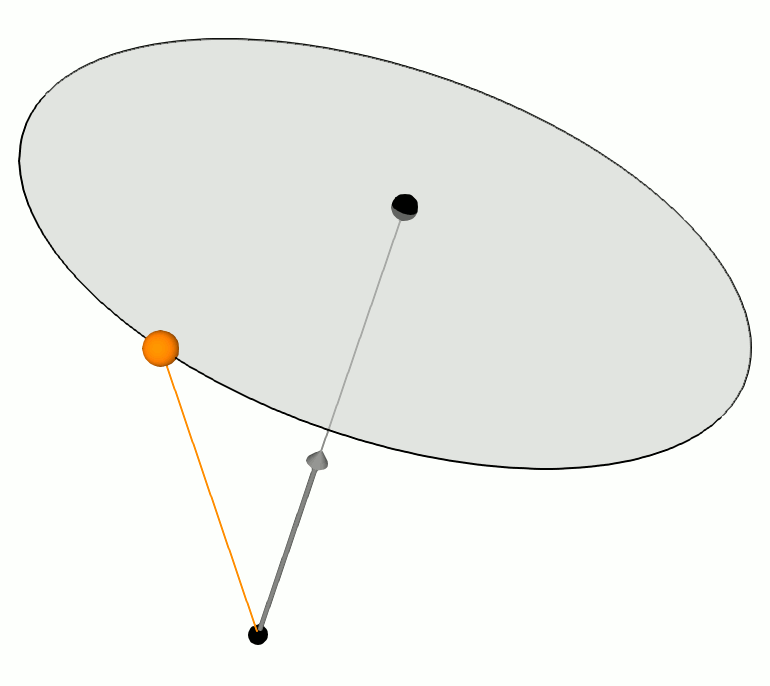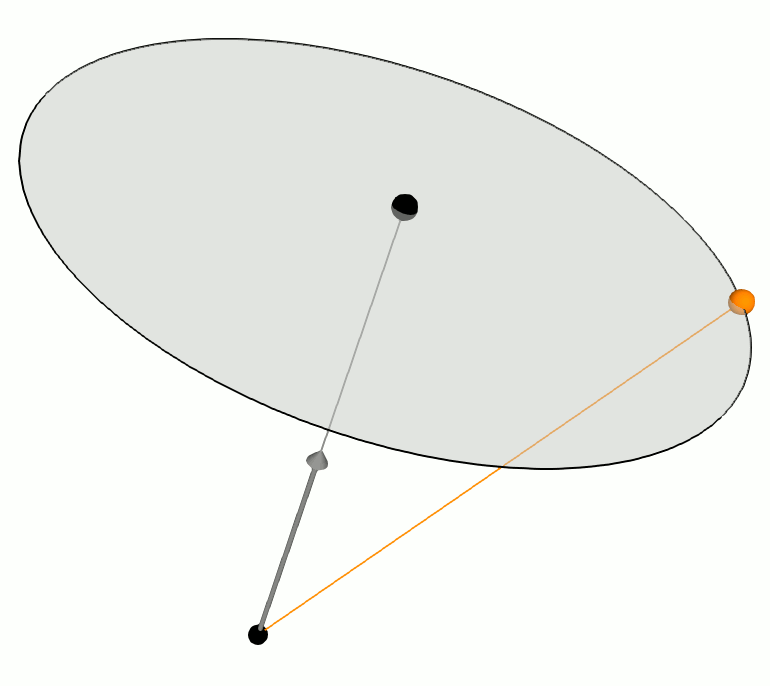
This page explains how to derive this rotation matrix from Rodrigues' rotation formula. Suppose a 3D point P is rotating to Q by an angle rotation angle along a unit vector rotation vector. The vector form of P is broken down the sum of vector OR and vector RP, and Q is the sum of vector OR and vector RQ respectively;
vector p , vector q

Therefore, we need to find vector OR and vector RQ first in order to get Q. The vector vector OR can be aquired from vector p, and vector RQ comes from the circular plane, where the point Q lies on. vector OR is parallel to the unit vector vector OR, and its length can be computed by projecting vector p to vector r using inner product. So, it can be written;
vector OR by dot product p and r
Rotation animation
Animation Of Rotating A Vertex About Arbitrary Axis
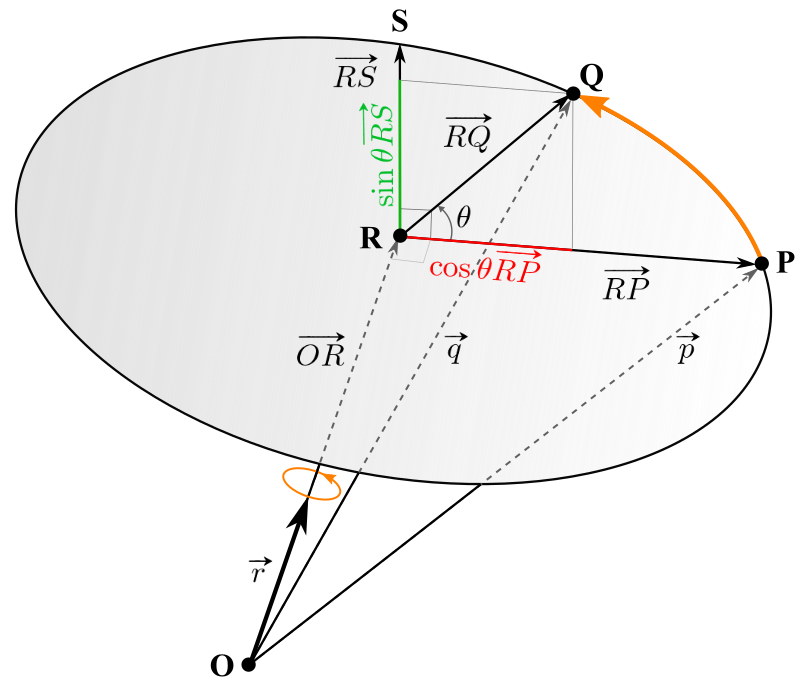
Diagram of rotation about arbitrary axis
Rotating P to Q About Arbitrary Axis

vector RQ can be determined by 2 basis vectors on the rotation plane. We use vector RP as the first basis vector, and the other basis vector vector RS is perpendicular to vector RP and has equal length because they are both the radius of the circluar plane. Therefore, vector RS can be computed by the cross product of 2 perpendicular vectors; vector r and vector RP;
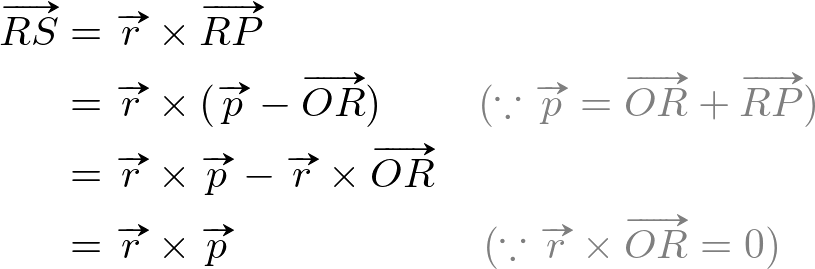
vector RS

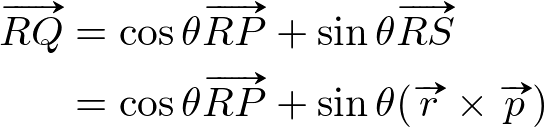
Now, vector RQ is represented with the composition of these basis vectors and trigonometric functions;
vector RQ

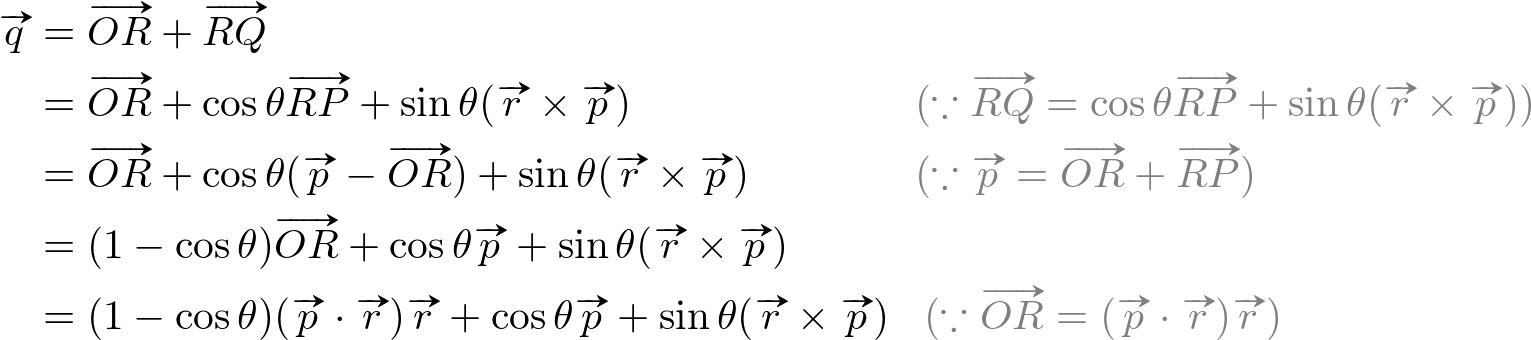
Finally, the rotated vector vector q is written by the sum of vector OR and vector RQ;
vector q

This equation is called Rodrigues' rotation formula;
Rodriues' Rotation Formula

It can be represented by an equivalent matrix form. First, convert vector OR and vector RS components to 3x3 matrix forms for P = (px, py, pz) and r = (x, y, z);
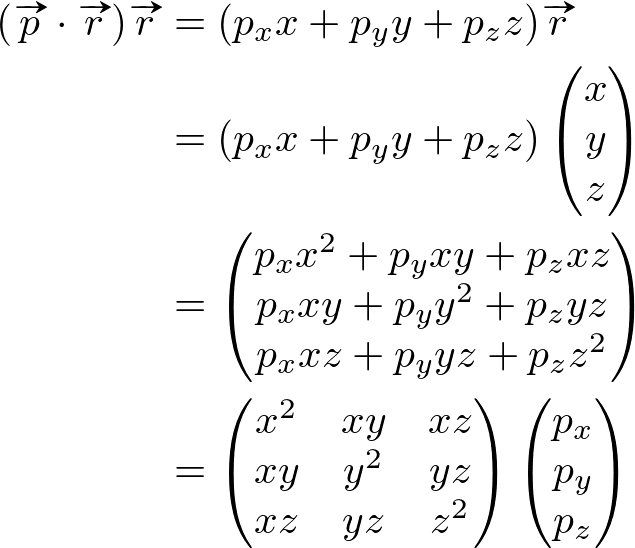
matrix form of OR

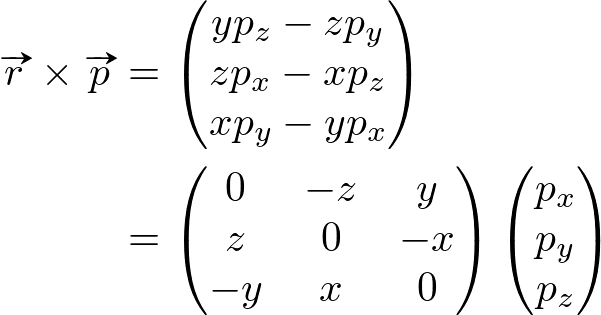
matrix form of RS

Finally, the equivalent matrix form by substituting the above matrix components is;
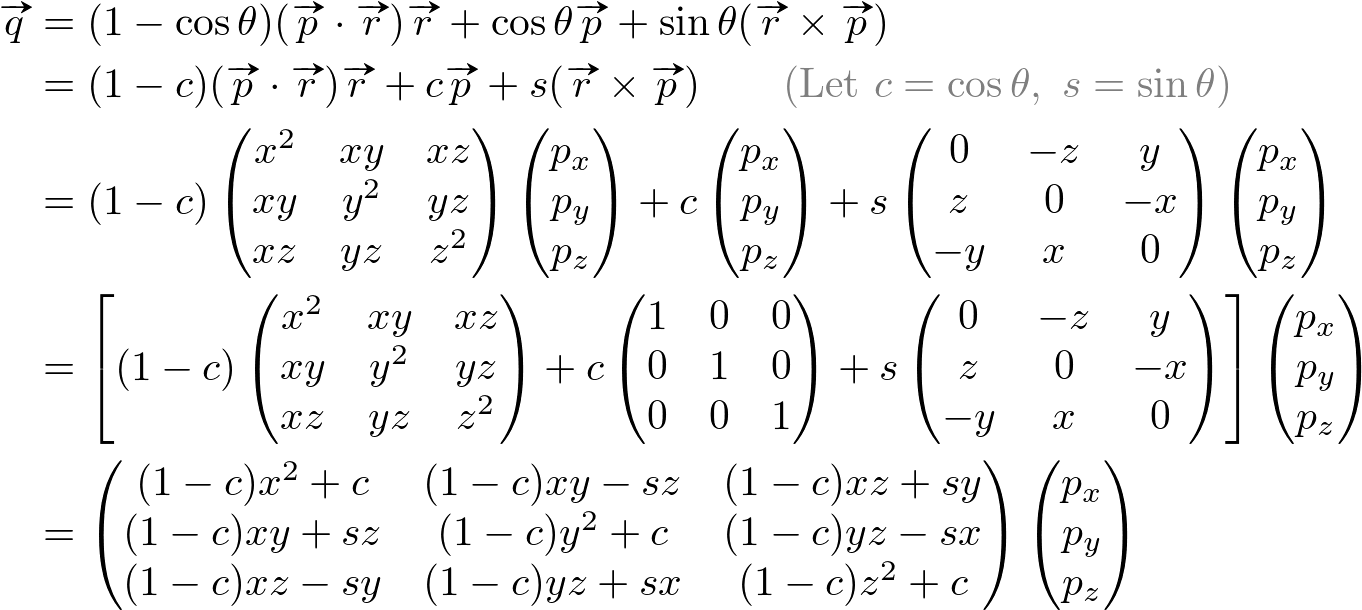
matrix form of q

And, the 3x3 rotation matrix alone is
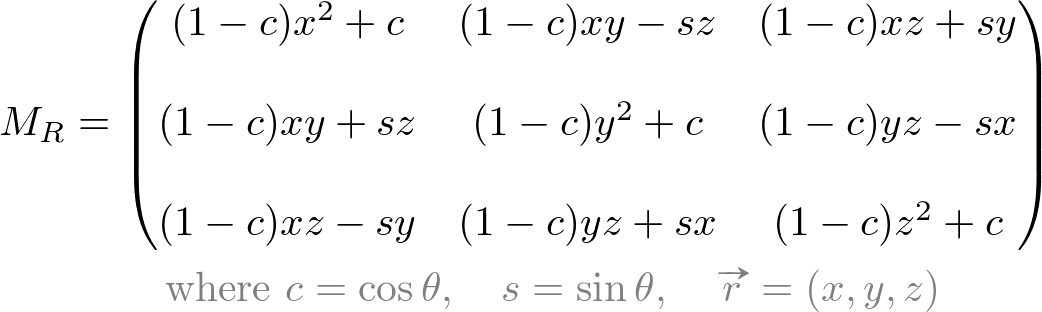
3x3 rotation matrix

Or, as 4x4 matrix;
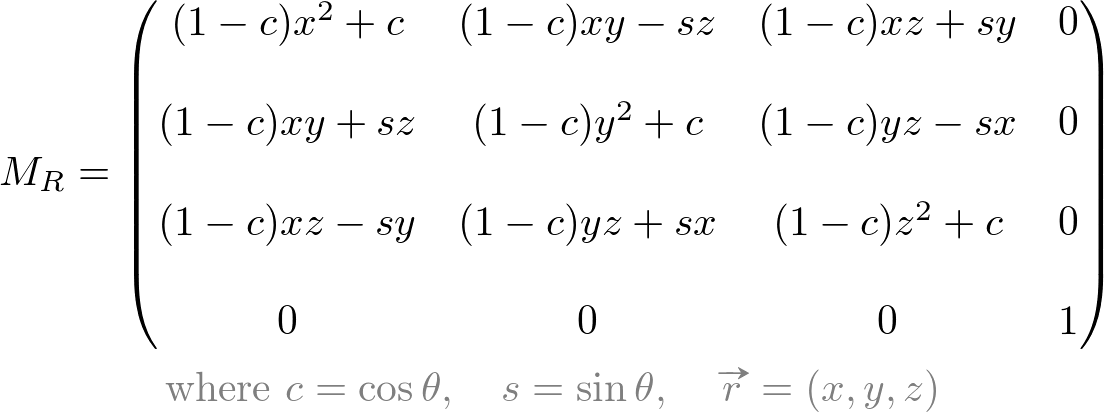
4x4 rotation matrix

Example: Rodrigues' Rotation Formula

The following C++ code snippet is rotating a 3D point P to Q along the rotation axis vector r using Rodrigues' formula. Download the complete implementation from rotate.zip.

rodrigues' formula 


// minimal implementation of Vector3
struct Vector3
{
    float x, y, z;
    // ctor
    Vector3() : x(0), y(0), z(0) {}

    // inner and cross products
    float   dot(Vector3& v)   { return x*v.x + y*v.y + z*v.z; }
    Vector3 cross(Vector3& v) { return Vector3(y*v.z-z*v.y, z*v.x-x*v.z, x*v.y-y*v.x); }
    // scalar product
    friend Vector3 operator*(float s, Vector3 v) { return Vector3(s*v.x, s*v.y, s*v.z); }
    Vector3& normalize() {
        float invLength = 1.0f / sqrtf(x*x + y*y + z*z);
        x *= invLength;
        y *= invLength;
        z *= invLength;
        return *this;
    }
}
...

// define the rotation vector r and angle
Vector3 r = Vector3(1, 1, 1).normalize();   // make unit length
float a = 30 / 180 * PI;                    // rotation angle as radian

// define a vector P to rotate
Vector3 p = Vector3(1, 2, 3);

// compute the rotated vector Q using Rodrigues' formula
Vector3 q = (1 - cos(a)) * p.dot(r) * r + cos(a) * p + sin(a) * r.cross(p);
←Back
 
Hide Comments
comments powered by Disqus