WebGL Vectors & Matrices
Related Topics: OpenGL Matrix, OpenGL Transform
Overview
To draw a 2D or 3D geometry on the screen, you need to define the vertex data in your application. These vertex data need to be transformed by model, view, and projection matrices. This vertex operation is performed in your vertex shader program, so the vertex data and transformation matrices are must be passed to the vertex shader program.

This page explains the most fundamental JavaScript classes to define the vertex data and transformations.
Vectors
Vector2, Vector3, and Vector4 classes are used to define 2D/3D/4D vertex positions, normals, colours, texture coordinates. Also, they are used to define lights and materials as well. The core interfaces of these classes follow.
Most of functions return the object reference (this) after the operations, so you can chain muliple function invocations sequentially. The complete source code is available at GitHub repository.
Vector2 class is typically to define 2D vertices or texture coordinates.
| Vector2 | |
|---|---|
| Function | Description |
| clone() | Make a copy of this and return a new instance of Vector2 |
| toFloat32Array() | Return this as a typed array (to pass this to WebGL) |
| set(x, y) | Update this with new (x, y) values |
| set(v) | Update this with a Vector2 |
| add(v) | Update this by adding with the given Vector2 |
| subtract(v) | Update this by subtracting with the given Vector2 |
| scale(s) | Update this by scaling with the given scalar |
| normalize() | Update this as a unit vector (length = 1) |
| dot(v) | Return inner product with this and the given Vector2 |
| distance(v) | Return the distance between this and the given Vector2 |
Vector3 class is typically used for a 3D vertex position or normal vector.
| Vector3 | |
|---|---|
| Function | Description |
| clone() | Make a new copy of this Vector3 instance |
| toFloat32Array() | Return this as a typed array (to pass this to WebGL) |
| set(x, y, z) | Update this with new (x, y, z) values |
| set(v) | Update this with a Vector3 |
| add(v) | Update this by adding with the given Vector3 |
| subtract(v) | Update this by subtracting with the given Vector3 |
| scale(s) | Update this by scaling with the given scalar value |
| dot(v) | Return inner product with this and the given Vector3 |
| Vector3.cross(v1,v2) | Return the cross product of 2 vectors (static function) |
| normalize() | Update this as a unit vector (length = 1) |
| distance(v) | Return the distance between this and the given Vector3 |
Vector4 class is used for a vertex (x, y, z, w) in homogeneous coordinates or color (r, g, b, a) to multiply by a 4x4 matrix.
| Vector4 | |
|---|---|
| Function | Description |
| clone() | Make a new copy of this Vector4 instance |
| toFloat32Array() | Return this as a typed array (to pass this to WebGL) |
| set(x, y, z, w) | Update this with new (x, y, z, w) values |
| set(v) | Update this with a Vector4 |
| add(v) | Update this by adding with the given Vector4 |
| subtract(v) | Update this by subtracting with the given Vector4 |
| scale(s) | Update this by scaling with the given scalar value |
| dot(v) | Return inner product with this and the given Vector4 |
| normalize() | Update this as a unit vector (length = 1) |
| distance(v) | Return the distance between this and the given Vector4 |
Here is an example of useage of the most common Vector3 class.
// define 2 vertices
let v1 = new Vector3(1, 2, 3);
let v2 = new Vector3(4, 5, 6);
// multiple operations in a sequence
v1.add(v2).subtract(v2).scale(2).normalize();
// dot and cross products
let dot = v1.dot(v2); // return scalar
let v3 = Vector3.cross(v1, v2); // return Vector3
// pass value to WebGL
gl.bufferData(gl.ARRAY_BUFFER, v1.toFloat32Array(), gl.STATIC_DRAW);
Matrices
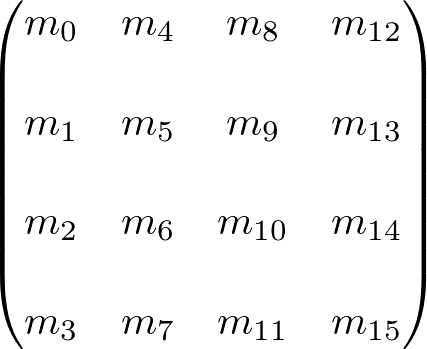
Matrices.js defines 3x3 and 4x4 matrices, but WebGL mainly uses 4x4 matrix to transform vertices; translation, rotation, scaling and projection.
The reason we are using 4x4 matrix instead of 3x3 is because of perspective projection. If a 3D point is projected on to a screen, it becomes a 2D point by loosing the depth value (z). Therefore, we begin with a 4D point (homogeneous coordinates) and transform by 4x4 projection matrix. Then, the projected point will be a 3D, which is still reserving the Z value. Please visit OpenGL Transformation page to learn how the vertex operations are performed in OpenGL/WebGL rendering pipeline.
Matrix4 class provides various functions for these transformations. It contains a typed array, Float32Array of 16 elements of a 4x4 square matrix as a column-major order notation (The first column of the matrx is stored first, then store the second column, and so on). Most functions return the object reference, this, so you can chain multiple functions in a row.
| Matrix4 | |
|---|---|
| Interface | Description |
| m | 1D Float32Array containing all 16 elements of this (Used to pass this to WebGL) |
| clone() | Make a new copy of this Matrix4 instance |
| getLeftAxis() | Return the left axis (Vector3) of this |
| getUpAxis() | Return the up axis (Vector3) of this |
| getForwardAxis() | Return the forward axis (Vector3) of this |
| getRotationMatrix() | Return a new Matrix4 containing only orientation part (Used to transform normals) |
| identity() | Update this as an identity matrix |
| transpose() | Update this by transpose |
| invert() | Update this by inverse |
| multiply(m) | Update this by multiplying with the given Matrix4 |
| translate(x, y, z) | Update this by translating with the given (x, y, z) |
| scale(x, y, z) | Update this by scaling with the given (x, y, z) |
| rotate(a, x, y, z) | Update this by rotating with the given angle and rotation axis (x, y, z) |
| rotateX(a) | Update this by rotating with the given angle along X-axis |
| rotateY(a) | Update this by rotating with the given angle along Y-axis |
| rotateZ(a) | Update this by rotating with the given angle along Z-axis |
| lookAt(tx,ty,tz, ux,uy,uz) | Update this by rotating to the given target (tx,ty,tz) and up vector (ux,uy,uz) |
| transform(v) | Return the transformed 3D or 4D vector after multiplying this and the given vector |
| Matrix4.makeFrustum(l,r,b,t,nf) | Construct a perspective matrix with (left, right, bottom, top, near, far) |
| Matrix4.makePerspective(fov,asp,n,f) | Construct a perspective matrix with (FOV, aspectRatio, near, far) |
| Matrix4.makeOrthographic(l,r,b,t,nf) | Construct an orthographic matrix with (left, right, bottom, top, near, far) |
If you want to know more about how the transform matrix is constructed in OpenGL or WebGL, please visit the following pages.
- Matrix4 transform functions
- How to rotate a vector along an arbitrary axis
- How to rotate a vector using Quaternion
- How to implement camera's lookAt()
- How to transform normal vectors
- How to construct the projection matrix
Here is a typical usage of Matrix4 class.
// construct model, view, projection matrices
let matrixModel = new Matrix4();
let matrixView = new Matrix4();
let matrixProjection = Matrix4.makePerspective(45, 1/1, 1, 1000); // fov, w/h, near, far
// transform model matrix
matrixModel.translate(1, 2, 3).rotateY(1.2); // radian
// transform view matrix
matrixView.translate(0, 0, -10).lookAt(1, 2, 3);
// construct ModelView matrix: V * M
let matrixMV = matrixView.clone().multiply(matrixModel);
// construct ModelViewProjection matrix: P * V * M
let matrixMVP = matrixProjection.clone().multiply(matrixView).multiply(matrixModel);
// construct Normal matrix
let matrixN = matrixView.getRotationMatrix();
// pass matrices to WebGL shader
gl.uniformMatrix4fv(program.uniform.matrixN, matrixN.m); // Normal
gl.uniformMatrix4fv(program.uniform.matrixMV, matrixMV.m); // ModelView
gl.uniformMatrix4fv(program.uniform.matrixMVP, matrixMVP.m); // ModelViewProjection